対流熱伝達
対流熱伝達による伝熱量を求めるには熱伝達率を求めておく必要があります。
ここでは熱伝達率を求めるために必要な知識準備をしていきます。
ヌセルト数
対流熱伝達は物体表面と移動している流体間で熱が伝わる現象です。その伝熱量はニュートンの冷却法則から求められます。
熱伝導は静止している固体・流体内で熱が伝わる現象です。その伝熱量はフーリエの法則から求められます。
ここで下の図のような流体の層を考えます。
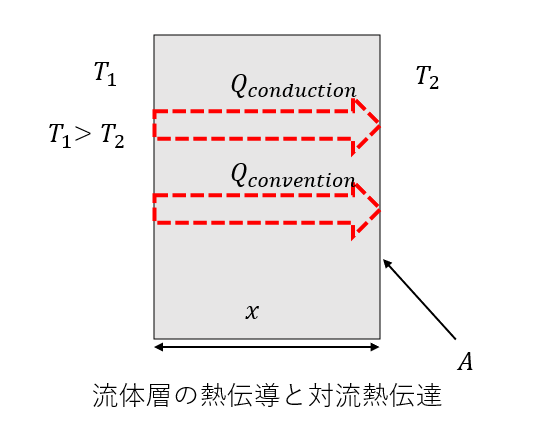
流体が静止しているとき熱伝導による伝熱量は \(\displaystyle Q_{conduction} = λ × \frac{T_1-T_2}{x} × A\)
流体が動いているとき対流熱伝達による伝熱量は \(Q_{convention} = h × (T_1-T_2) × A\)
と表せます。
\(\displaystyle Nu = \frac{Q_{convention}}{Q_{conduction}} = \frac{hx}{λ}\)
このとき\(Nu\)をヌセルト数といいます。\(Nu\)は熱伝導に比べて熱伝達による伝熱量がどのくらい大きくなっているかを示し、\(Nu\)が大きいほど熱伝達による伝熱が増加することを表します。
ヌセルト数Nuは無次元熱伝達率ともいいます。
境界層
対流熱伝達は物体表面に近いほどこの表面から影響を受け、遠ざかるにつれて影響を受けにくくなります。
この領域を境界層といいます。
境界層には速度境界層と温度境界層があります。
速度境界層
速度境界層のイメージ図を下に示します。
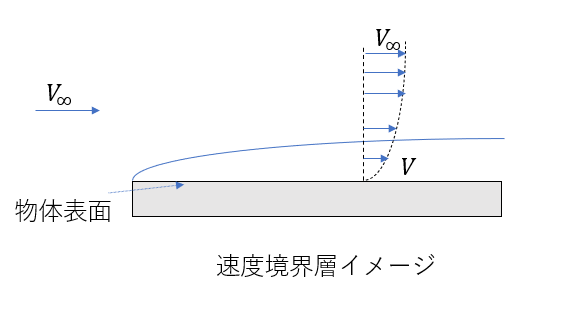
物体表面から垂直方向に離れるにつれて表面上の流体の流れは影響を受けにくくなります。流体の流れが影響を受ける領域を速度境界層といいます。\(V_∞\)を物体から十分に離れた距離にある主流温度とすると、流体の流速\(V\)は物体表面から離れるにつれて\(V_∞\)に近づいていきます。\(V\)が\(V_∞\)の99%のときの物体表面からの距離を速度境界層厚さといいます。
速度境界層厚さは下流に行くほど、また粘度が大きいほど厚くなります。
温度境界層
温度境界層のイメージ図を下に示します。この例では\(T>T_∞\)のときを考えます。
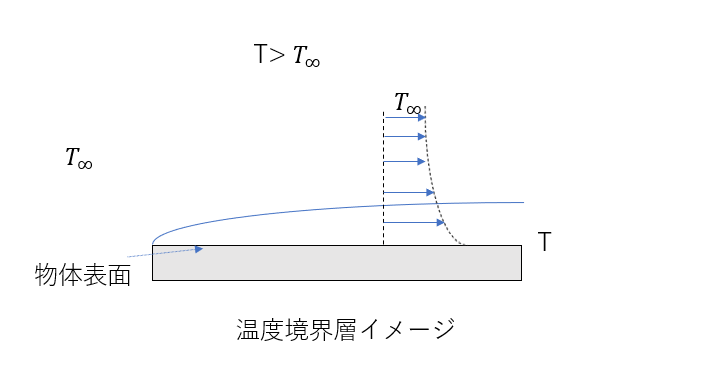
\(T>T_∞\)のとき物体表面周辺の流体の温度は物体表面から影響を受けます。\(T_∞\)を物体から十分に離れたところの温度(主流温度)、\(T\)を物体表面の温度とすると、表面周辺の流体の温度は表面から離れるにつれて\(T_∞\)に近づきます。
\(T\)が\(T_∞\)の99%のときの物体表面からの距離を温度境界層厚さといいます。
温度境界層厚さは下流へ行くほど流体が加熱されるので厚くなります。
プラントル数
速度境界層と温度境界層の関係は対流熱伝達の熱伝達率に大きな影響を与えます。
この関係を表す無次元数をプラントル数\(P_r\)といいます。
プラントル数\(P_r\)は
\(\displaystyle P_r = \frac{ν}{a} = \frac{ηC}{λ} \)
と表せます。
νは動粘度[\(m^2/s\)]、aは熱拡散率[\(m^2/s\)]、ηは粘度[Pa・s]、Cは定圧比熱[J/kg・K]、λは熱伝導率[W/m・K]です。
プラントル数は速度変化と温度変化のしやすさを表します。Pr > 1だと温度変化がしやすく(速度境界層が温度境界層より厚く)、Pr < 1だと速度変化がしやすい(温度境界層が速度境界層より厚い)です。
層流と乱流
流体の流れには層流と乱流があります。蚊取り線香の例で考えましょう。
火のついている蚊取り線香から煙が出ているのを見たことがある人は多いと思います。
あの煙の動きを思い出してみてください。
煙が火元から立ち上がるとき、始めは一つの線のようなまっすぐな煙が立ち上がります。
その後次第に煙が渦巻いていきます。始めのまっすぐな流れを層流といいます。
そして、渦巻いた流れを乱流といいます。
たばこやマッチの煙も同じ現象が見られます。
では、どこで層流と乱流に分かれるのでしょうか。
その分類にレイノルズ数が用いられます。
レイノルズ数
レイノルズが層流か乱流かは、流体の流れの慣性力と粘性力の比で決まることを示しました。
この比をレイノルズ数\(Re\)といいます。
レイノルズ数\(Re\)は
\(\displaystyle Re = \frac{VL_c}{ν}\)
と表せます。
\(L_c\)は代表長さといいます。これは流体の流れに沿った方向の長さです。
分子の\(VL_c\)が慣性力、分母のνが粘性力に依存する項になっています。レイノルズ数が大きいと乱流になります。
レイノルズ数が大きいときは慣性力が粘性力に比べて大きく、慣性の流れを粘性力で抑えきれないので乱流になります。
レイノルズ数が小さいときは逆で、慣性の流れを粘性力で抑えられるので層流になります。
- 層流が乱流になるレイノルズ数はありますか?
-
あります。層流が乱流になるときのレイノルズ数を臨界レイノルズ数や遷移レイノルズ数といいます。
円管の流れではこの値は2300程度です。この値は形状や流れ状態により異なります。 - ~数が多すぎます。
-
私もそう思います。・・・少しずつ慣れるしかありません。今回紹介したヌセルト数、プラントル数、レイノルズ数は実用上特に重要な用語です。
- ヌセルト数\(\displaystyle N_u = \frac{Q_{convention}}{Q_{conduction}} = \frac{hx}{λ} = Nu\)
- プラントル数\(\displaystyle P_r = \frac{ν}{a} = \frac{ηC}{λ} \)
- レイノルズ数\(\displaystyle R_e = \frac{VL_c}{ν}\)
これでようやく熱伝達率を求める準備ができました。
次回は実際に熱伝達率を求めてみましょう。
