熱伝達率計算方法
対流による伝熱量はニュートンの冷却法則から求められます。
伝熱量を求めるには熱伝達率がわからないと求められません。
ここでは対流の伝熱量を求めるのに必要な熱伝達率の求め方を解説します。
熱伝達率計算手順
熱伝達率は次の手順で求めていきます。
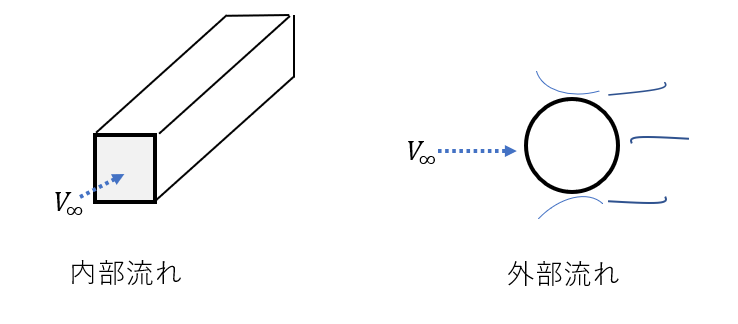
まず初めに熱伝達率を求めたい対象の形状や流体の種類、流れを決定します。流れには内部流れと外部流れが存在します。内部流れはダクトなどの管で流路が制限されている流れのことです。外部流れは流路が制限されていない流れのことです。下にそれぞれのイメージ図を示します。
対流の種類を確認します。計算対象が外部から影響を受けない自然対流になっているのか、ファンなどの送風の影響を受けている強制対流になっているかです。
内部流れは平均混合温度、外部流れは膜温度の温度に対応する物性値を準備します。
物性値は調べるか計算して準備します。平均混合温度と膜温度については下に記載しています。
物性値からレイノルズ数(もしくはレイリー数)を求め、層流か乱流かを決定します。自然対流の場合は層流か乱流かを決定する数がレイリー数になります。レイリー数の詳細はこの記事で後ほど解説します。
ここでは、ここまでに計算してきた値から計算対象に適応する相関式を選択し、ヌセルト数を求めます。
ヌセルト数が求まったので、この値を用いて熱伝達率を求めます。
これでようやく対流熱伝達による伝熱量を求める準備ができました。
Step2の内部流れと外部流れについて
流れには流路が制限されているかどうかによって内部流れと外部流れに分かれています。
内部流れはダクトのように流路が制限されており、温度境界層や速度境界層が自由に発達しない流れです。
外部流れは球の表面の流体の流れのように流路が制限されず、温度境界層や速度境界層が自由に発達する流れです。
上のStep3に用いる温度は、内部流れの場合は平均混合温度。外部流れの場合は膜温度を使用します。
平均混合温度 \(T_b\)
\(T_b = \frac{T_i + T_e}{2}\)
です。\(T_i\)は菅入口の流体の平均温度、\(T_e\)は菅出口の流体の平均温度です。
膜温度\(T_f\)
\(T_f = \frac{T + T_∞}{2}\)
です。\(T\)は物体伝熱面の温度、\(T_∞\)は主流温度です。
物性値について
温度ごとの空気の物性値は別の記事にまとめますのでご参照ください。
レイリー数
強制対流では層流か乱流かが決まる指標がレイノルズ数でした。
自然対流の場合は層流か乱流かが決まる指標をレイリー数\(Ra_L\)といいます。
レイリー数\(Ra_L\)は
\(\displaystyle Ra_L = \frac{gβ(T – T_∞)L_c^3}{ν^2}Pr\)
と表せます。
βは体積膨張率[\(K^{-1}\)]といいます。空気のような理想気体の場合は
\(\displaystyle β = \frac{1}{T_∞}\)
と表せます。
gは重力加速度[\(m/s^2\)]です。
熱伝達率を求めるのは慣れるまでは複雑だと感じると思いますが、手順を確認しながらゆっくり計算してみてください。
これで熱伝達率を求める準備ができました。
次回は具体例で熱伝達率と伝熱量を求めます。
