強制対流による伝熱量の計算
ここでは強制対流外部流れの伝熱量の計算をします。
そのためには、熱伝達率を求めておく必要があります。
前々回に紹介した以下の熱伝達率の求め方の手順に従って具体例を用いて計算していきます。
平板の場合
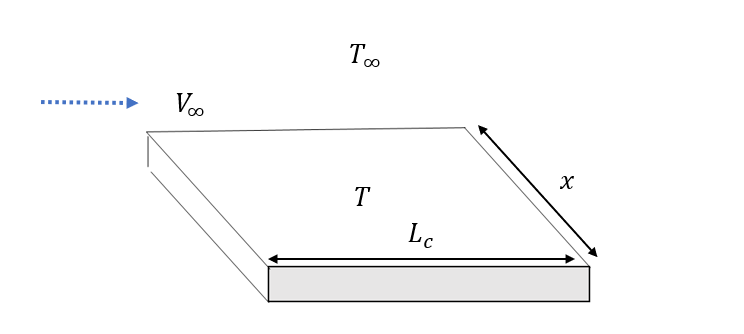
図のような平板の例を考えます。平板の表面温度\(T\) = 320[K]、主流温度\(T_∞\) = 300[K]、
主流速度\(V_∞\)=2[m/s]、流れ方向の平板の長さ\(L_c\) = 2[m]、平板の幅\(x\) = 1[m]、臨界レイノルズ数は\(5×10^5\)とします。
STEP1~STEP6の順に熱伝達率を求めていきます。
STEP1:この例では平板を考えるので、計算対象は平板です。
STEP2:上の図の向きに流速Vの空気の流れがありますので、強制対流です。
STEP3:膜温度から物性値を準備します。
膜温度\(T_f\)
\(T_f = \frac{T + T_∞}{2}\)で求められます。
STEP3の温度は、内部流れの場合は平均混合温度。外部流れの場合は膜温度を使用します。
平均混合温度 \(T_b = \frac{T_i + T_e}{2}\)
\(T_i\)は菅入口の流体の平均温度、\(T_e\)は菅出口の流体の平均温度です。
膜温度\(T_f = \frac{T + T_∞}{2}\)
\(T\)は物体伝熱面の温度、\(T_∞\)は主流温度です。
平板の例では外部流れなので膜温度を使用します。
\(T_f = \frac{T + T_∞}{2} = \frac{320 + 300}{2} = 310[K]\)と求められますので、310Kのときの空気の物性値を計算に用います。310Kのときの物性値は動粘度ν = 16.845×\(10^{-6}[m^2/s]\)、熱伝導率λ = 23.445×\(10^{-3}\)[W/m・K]、
プラントル数Pr = 0.718[-]です。空気の物性値は別の記事(https://fujitart.com/wp-admin/post.php?post=814&action=edit)にまとめてますので、その値を参照しています。
STEP4:層流か乱流かを確認します。
\(L_c\) = 4のときのレイノルズ数Reは
\(Re = \frac{V_∞L_c}{ν} = \frac{2×2}{16.845×10^{-6}} = 2.37×10^5\)
計算の結果、
レイノルズ数 \(2.37×10^5\) < 臨界レイノルズ数\(5×10^5\)なので、平板上の流れは層流とわかりました。
STEP5:STEP1~4で計算する条件がわかったので、計算対象に適応する相関式からヌセルト数Nuを求めます。
全体が等温加熱されている平板の外部流れのヌセルト数を求める式は下記の式です。
流れが層流か乱流か、もしくはそれらが混在しているかにより、式が異なります。
- 層流の場合
\(\displaystyle Nu = 0.664Re^{1/2}Pr^{1/3} = \frac{hL_c}{λ} (Re < 5×10^5)\) - 乱流の場合
\(\displaystyle Nu = 0.037Re^{4/5}Pr^{1/3} = \frac{hL_c}{λ} (0.6 \leq Pr \leq 60, 5×10^5 \leq Re \leq 10^7)\) - 層流と乱流が混在している場合
\(\displaystyle Nu = (0.037Re^{4/5} – 871)Pr^{1/3} = \frac{hL_c}{λ} (0.6 < Pr < 60, 5×10^5 < Re < 10^7)\)
今回の対象は一つ目の式に合致するので、この層流の場合の式からヌセルト数Nuを求めます。
\(\displaystyle Nu = 0.664Re^{1/2}Pr^{1/3} = 0.664×(2.37×10^5)^{1/2}×0.718^{1/3} = 289.46\)
ヌセルト数Nu = 289.46より、熱伝達率hは
\(h = Nu × \frac{λ}{L_c} = 289.46×\frac{23.445×10^{-3}[W/m・K]}{2[m]} = 3.39[W/m^2・K]\)
ようやく熱伝達率hが求まりました。
熱伝達率がわかったので、伝熱量Qはニュートンの冷却法則から求められます。
\(Q = h × (T – T_∞) × A = 3.39[W/m^2・K] × (320 – 300)[K] × 2 × 1[m^2] = 135.6[W]\)
平板からの伝熱量は135.6Wと求まります。
円柱の場合
続いて円柱の場合の強制対流熱伝達の伝熱量の計算をします。
具体例の前に図のように円柱の周りに空気が流れているときのレイノルズ数とヌセルト数の求め方についてまとめます。
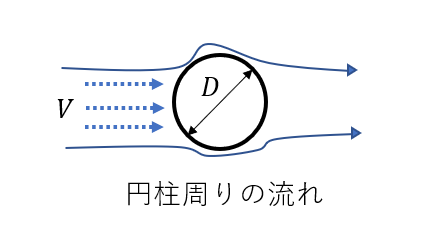
円柱周りの流れのレイノルズ数\(Re_D\)は流速Vと円柱直径Dを用いて次の式から求められます。
\(\displaystyle Re_D = \frac{VD}{ν}\)
円柱や球の周りの臨界レイノルズ数はだいたい\(2×10^5\)です。
気体や液体の流れの中にある円柱の表面平均ヌセルト数\(Nu_D\)を求める相関式はChurchill – Bernsteinの式が提示されています。
\(\displaystyle Nu_D = 0.3 + \frac{0.62Re_D^{1/2}Pr^{1/3}}{{[1 + {(0.4/Pr)}^{2/3}]}^{1/4}}{[1 + {(\frac{Re_D}{282000})}^{5/8}]}^{4/5} = \frac{hD}{λ} (Re_DPr > 0.2)\)
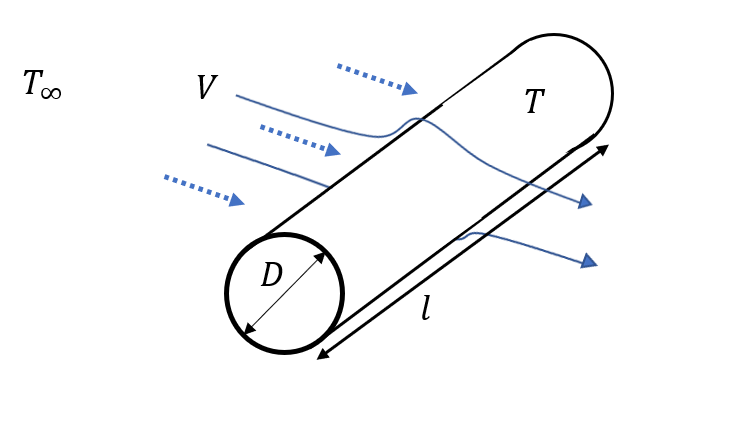
ここでは、下の図のように空気の流れに円柱が垂直置かれているときの伝熱量を求めます。
T = 320[K]、 \(T_∞\) = 300[K]、 V = 2[m/s]、 D = 20[mm]とします。
対流の伝熱量を求めるには熱伝達率を求める必要があります。
平板の例と同様にSTEP1~STEP6の順に熱伝達率を求めていきます。
STEP1:この例では円柱を考えるので、計算対象は円柱です。
STEP2:上の図の向きに流速Vの空気の流れがありますので、強制対流です。
STEP3:膜温度から物性値を準備します。
膜温度\(T_f = \frac{T + T_∞}{2} = \frac{320 + 300}{2} = 310[K]\)
310Kのときの空気の物性値を計算に用います。310Kのときの物性値は動粘度ν = 16.845×\(10^{-6}[m^2/s]\)、
熱伝導率λ = 23.445×\(10^{-3}\)[W/m・K]、プラントル数Pr = 0.718[-]です。
STEP4:層流か乱流かを確認します。
円柱表面のレイノルズ数\(Re_D\)は
\(\displaystyle Re_D = \frac{VD}{ν} = \frac{2×20×10^{-3}}{16.845×10^{-6}} = 2374.59\)
計算の結果、
レイノルズ数 2374.59 < 臨界レイノルズ数\(2×10^5\)なので、平板上の流れは層流とわかりました。
STEP5:STEP1~4で計算する条件がわかったので、計算対象に適応する相関式からヌセルト数Nuを求めます。
Churchill – Bernsteinの式が適用できるので、
\(\displaystyle Nu_D = 0.3 + \frac{0.62Re_D^{1/2}Pr^{1/3}}{{[1 + {(0.4/Pr)}^{2/3}]}^{1/4}}{[1 + {(\frac{Re_D}{282000})}^{5/8}]}^{4/5} = 0.3 + \frac{0.62×2374.59^{1/2}0.718^{1/3}}{{[1 + {(0.4/0.718)}^{2/3}]}^{1/4}}{[1 + {(\frac{2374.59}{282000})}^{5/8}]}^{4/5} \) = 25.029
ヌセルト数\(Nu_D\) = 25.029なので熱伝達率hは
\(h = \frac{λ}{D}×Nu_D = \frac{23.445×10^{-3}[W/m・K]}{20×10^{-3}[m]} ×25.029 = 29.34[W/m^2・k]\)
ニュートンの冷却法則から伝熱量Qは
\(Q = h × (T – T_∞) × A = 29.34[W/m^2・K] × (320 – 300)[K] × 20×10^{-3}× π × l[m^2] = 36.87l[W]\)
だと求められます。
単位長さ当たりの伝熱量Q/lは36.87[W/m]です。
具体例2つで伝熱量の計算をしました。計算の流れは基本的には同じです。伝熱量の計算では相関式の選択が重要だと著者は感じています。設計での実用性を考えると、計算対象を相関式が適用できそうな形状に近似して
ある程度の伝熱量が手計算できることが役立ちます。数値シミュレーションを使用する前にも形状の当たりをつけたり、だいたいの伝熱量があらかじめわかると、数値シミュレーションの手間が減り設計効率化が見込めます。
この記事では対流熱伝達の外部流れを考えました。
次回は内部流れについてです。
