強制対流による内部流れの熱伝達率の計算
前回は、強制対流の外部流れの伝熱量の計算をしました。
今回は、強制対流の内部流れを見ていきます。内部流れはその名の通り対象の内部の流れに着目して、そのときの熱伝達率を求め、最後に温度分布を求めます。
事前準備
内部流れの熱伝達率を計算するに当たり必要な知識の準備をしておきます。
平均混合温度
初めに円管の内部の温度のイメージ図を示します。
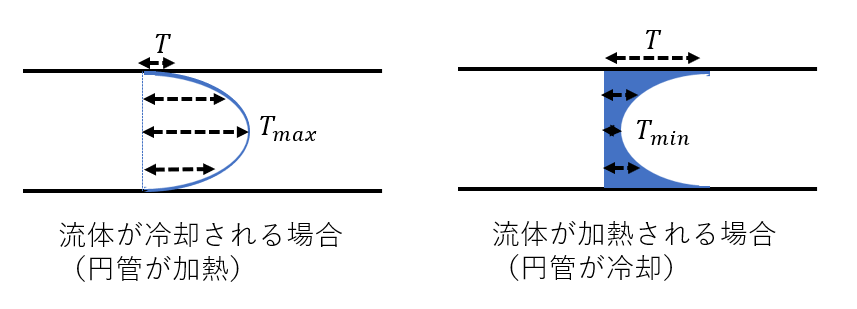
内部流れでは、円管の内部の温度が場所によって異なります。流体が冷却される場合は円管の内側から外側へかけて温度が低くなっており、中心が最高温度になっています。一方、流体が加熱される場合は円管の内側から外側へかけて温度が高くなっており、中心が最低温度となります。
では、物性値はどの温度を用いればいいのでしょうか?
平均温度は流れに沿って変化するため、これを使うことはできません。なので通常は管入口の温度\(T_i\)と、管出口の温度\(T_e\)の平均値である混合平均温度\(T_b\)を用います。
\(T_b = \frac{T_i + T_e}{2}\)
です。
外部流れでは膜温度を用いたのに対し、内部流れでは物性値の温度は平均混合温度を用いる。
平均流速
外部流れの計算では、主流速度を用いて計算していましたが、内部流れでは主流速度を用いることができません。
そこで、平均流速\(V_m\)を用います。
質量保存の法則から
\(\dot{m} = ρV_mA_c\)
と表せます。
\(\dot{m}\)は質量流量[kg/s]、ρは流体の密度[kg/\(m^3\)]、\(A_c\)は流路断面積\([m^2]\)です。
レイノルズ数と水力直径
内部流れの場合も外部流れと同様に、層流や乱流になります。
管内流のレイノルズ数Reは次の式から求められます。
\(\displaystyle Re = \frac{V_mD_h}{ν}\)
\(D_hは水力直径[m]\)といいます。
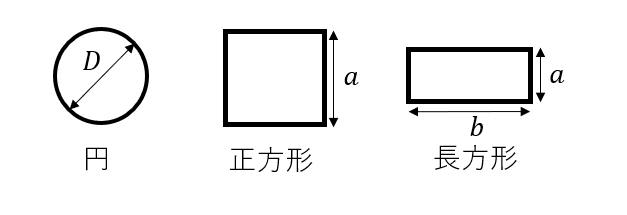
水力直径について
水力直径は等価直径ともいいます。これは正方形や長方形といった断面形状を円の直径として置き換えたものです。
水力直径を用いることで正方形や長方形も円と同じようにレイノルズ数を求められます。
\(D_h = \frac{4A_c}{p}\)
水力直径\(D_h\)は流路断面積\(A_c[m^2]\)と流路の周長p[m]から求められます。
- 円の場合
\(D_h = D\) - 正方形の場合
\(D_h = a\) - 長方形の場合
\(D_h = \frac{2ab}{a + b}\)
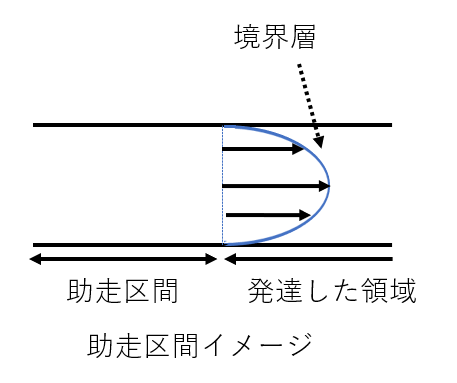
助走区間
流体は管内に入ると少しずつ境界層が発達していきます。管内入口から境界層が発達するまでの区間を助走区間といいます。
その長さを助走区間長さといいます。
下に助走区間のイメージ図を示します。
境界層には速度境界層と温度境界層があるので、それぞれ速度助走長さと温度助走長さがあります。
助走区間の先は発達した領域といいます。
助走長さは実験で求められた次の式で求められます。
層流の場合
速度助走長さ \(\simeq 0.05ReD_h\)
温度助走長さ \(\simeq 0.05RePrD_h\)
乱流の場合
速度助走長さ \(\simeq\) 温度助走長さ \(\simeq 10D_h\)
内部流では多くの場合が乱流であることに加えて、円管やダクトの長さは直径より十分大きいことが
ほとんどなので、このサイトでは発達した領域だと仮定して計算します。
内部流れの計算の準備ができたのでこれらの知識を踏まえて計算します。
ダクトの場合
これまでの知識を踏まえて下の図のようなダクトの温度分布を計算してみましょう。
入口の温度\(T_i\) = 340[K]、内壁の温度\(T_s\) = 320[K]、空気が体積流量V = 0.1[\(m^3/s\)]でダクトへ流入しており、ダクトの1辺の長さはa = 0.1[m]、長さL = 10[m]とします。
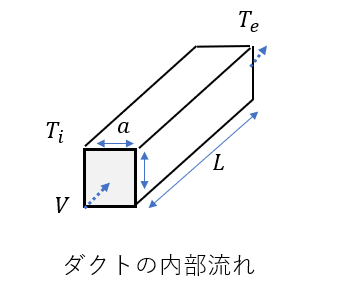
出口の温度はわからないので(T_e) = 300[K]と仮定します。
混合平均温度\(T_b = \frac{340 + 300}{2} = 320[K]\)です。
320[K]における空気の物性値は動粘度ν = 17.86×\(10^{-6}[m^2/s]\)、熱伝導率λ = 27.59×\(10^{-3}\)[W/m・K]、
プラントル数Pr = 0.719[-]、定圧比熱\(C_p = 1.008[kJ/kgK]\)、密度ρ = 1.102\([kg/m^3]\)です。
空気の物性値は別の記事(https://fujitart.com/wp-admin/post.php?post=814&action=edit)にまとめてますので、その値を参照しています。
水力直径は\(D_h = a = 0.1[m]\)、
伝熱面積\(A_s\)はダクトの周長と長さの積なので、
\(A_s = 4aL = 4×0.1[m]×10[m] = 4[m^2]\)
空気の平均流速\(V_m\)は体積流量Vとダクトの断面積の商なので、
\(V_m = 0.1[m^3/s]/(0.1×0.1[m^2]) = 10[m/s]\)
質量流量\(\dot{m} = ρV = 1.102[kg/m^3]×0.1[m^3/s] = 0.1102[kg/s]\)
レイノルズ数Reを求めると、
\(Re = \frac{V_m D_h}{ν} = \frac{10[m/s]×0.1[m]}{17.86×10^{-6}[m^2/s]} = 55991\)
Re > 2300より、内部の流れは乱流だとわかります。
乱流のときの助走区間長さは\(10D_h = 10×0.1 = 1[m]\)です。この値はダクトの長さに比べて十分小さいので、
ダクト全体が十分発達した領域だと考えられます。
次に平均ヌセルト数と平均熱伝達率を求めます。
発達した領域で、熱流束と内壁温度が一定の管内流れの平均ヌセルト数はDittus-Boelterの式から求められます。
\(Nu = \frac{hD_h}{λ} = 0.023Re^{0.8}Pr^n (0.7 \leq Pr \leq 160, Re > 10^4)\)
加熱のとき n = 0.4
冷却のとき n = 0.3を使います
Dittus-Boelterの式を用いて、\(Nu = 0.023Re^{0.8}Pr^n = 0.023×55991^{0.8}×0.719^{0.3} = 130.99\)
\(h = \frac{Nuλ}{D_h} = \frac{130.99×27.59×10^{-3}[W/mK]}{0.1[m]} = 36.14[W/m^2K]\)
熱伝達率が求まりました。
内壁温度\(T_s\)が一定の場合の平均温度分布は次の式で求められます。
\(T_m(x) = T_s – (T_s – T_i)exp(\frac{-hpx}{\dot{m}C_p})\)
xは管入口からの長さ、pは周長です。
したがって、平均温度は
\(T_m(x) = 320[K] – (320 – 340)exp(\frac{-36.14[W/m^2K]×4×0.1x}{0.1102[kg/s]×1.008[kJ/kgK]})\)
= 320 + 20 ×exp(-0.13014x)
この結果から平均温度分布が求められます。
| X[m] | 0 | 2 | 4 | 6 | 8 | 10 |
| \(T_m(x)[m]\) | 340 | 335.4167 | 331.8838 | 329.1604 | 327.0612 | 325.443 |
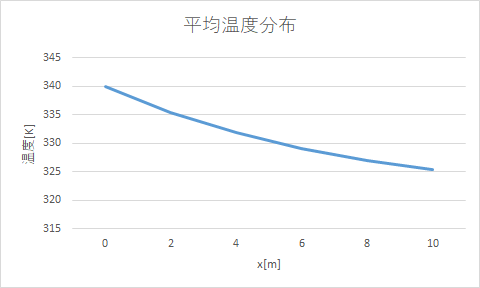
x = 10のときの温度は325.443[K]だとわかりました。今回初めに管の出口は300[K]だと仮定して計算しています。
約25[K]の差がありますので、出口の温度を325[K]として計算しなおすことでより正確な計算ができます。
計算しなおしが必要かどうかはどこまでの精度を求めているかによります。
ここまで内部流れの計算をしてきました。
多くの値が出てきて混乱しますが、何を計算しているかわからなくなった時は単位を見直すようにしてください。
単位をおさえておくことで計算が明確になります。
