温かいコーヒーを机の上に置いておくと少しずつ冷めていきます。これは自然対流による熱伝達が発生しています。
ここでは自然対流を見ていきます。

対流熱伝達には強制対流と自然対流があります。自然対流はその名の通り、自然な状態（外部から風などの影響を受けない）ときです。強制対流について詳しく知りたいかたは別の記事で紹介しているのでそちらを見てみてください。

下の図のように平板があるとします。

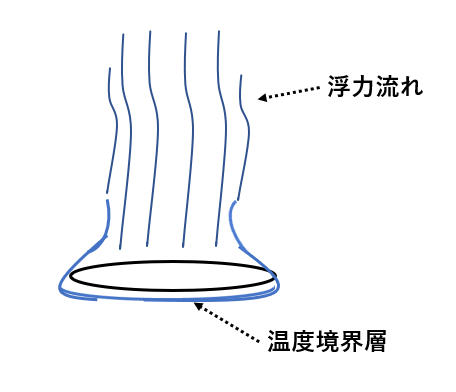
上の図のように物体と物体の周囲の流体との温度差によって、温度境界層内外の流体に密度差が生じます。
この密度差によって浮力流れが生じます。この浮力流れによって起こる対流を自然対流と言います。

周囲流体より高温の物体を置けば、物体近傍の流体は温度が高くなり、膨張し、密度が小さくなるので、浮力が生じて上向きの流れが起こります。逆に低温の物体は下向きの流れになります。

浮力の大きさは温度によって決まります。上記のように温度差によって密度が変化し、浮力が生じます。

定圧のときの温度による流体密度変化を示すのが、体積膨張率βです。

流体が空気のような理想気体の場合、

\(β =\frac{1}{T_∞}[K^{-1}]\)

と表せます。\(T_∞\)は主流温度です。

浮力は定圧の場合、温度差に比例します。

自然対流でも強制対流のときと同様に相関式から熱伝達率を求めます。

自然対流熱伝達ではグラスホフ数とレイリー数が相関式に用いられます。

グラスホフ数

グラスホフ数\(Gr_L\)は浮力と粘性力との比を表します。

\(Gr_L = \frac{浮力}{粘性力} = \frac{gβ(T_s – T_∞)L_c^3}{ν^2}\)

gは重力加速度\([m/s^2]\)、βは体積膨張率\([K^{-1}]\)、\(L_c\)は代表長さ[m]、νは動粘度\([m^2/s]\)です。

レイリー数

レイリー数は層流か乱流かを決める指標です。強制対流ではこの指標はレイノルズ数でした。

レイリー数はグラスホフ数とプラントル数の積で表されます。

\(Ra_L = Gr_LPr = \frac{gβ(T_s – T_∞)L_c^3}{ν^2}Pr\)